Anthony Williams from Just Software Solutions Blog
"Friendship" in C++ is commonly thought of as a means of allowing non-member
functions and other classes to access the private data of a class. This might be
done to allow symmetric conversions on non-member comparison operators, or allow
a factory class exclusive access to the constructor of a class, or any number of
things.
However, this is not the only use of friendship in C++, as there is an
additional property to declaring a function or function template a friend: the
friend function is now available to be found via Argument-Dependent Lookup
(ADL). This is what makes operator overloading work with classes in different
namespaces.
Argument Dependent Lookup at Work
Consider the following code snippet:
namespace A{
class X{
public:
X(int i):data(i){}
private:
int data;
friend bool operator==(X const& lhs,X const& rhs){
return lhs.data==rhs.data;
}
};
}
int main(){
A::X a(42),b(43);
if(a==b) do_stuff();
}
This code snippet works as you might expect: the compiler looks for an
implementation of operator== that works for A::X objects, and there isn't
one in the global namespace, so it also looks in the namespace where X came
from (A), and finds the operator defined as a friend of class X. Everything
is fine. This is ADL at work: the argument to the operator is an A::X
object, so the namespace that it comes from (A) is searched as well as the
namespace where the usage is.
Note, however, that the comparison operator is not declared anywhere other
than the friend declaration. This means that it is only considered for name
lookup when one of the arguments is an X object (and thus is "hidden" from
normal name lookup). To demonstrate this, let's define an additional class in
namespace A, which is convertible to 'X':
namespace A{
class Y{
public:
operator X() const{
return X(data);
}
Y(int i):data(i){}
private:
int data;
};
}
A::Y y(99);
A::X converted=y; // OK
Our Y class has a conversion operator defined, so we can convert it to an X
object at will, and it is also in namespace A. You might think that we can compare Y
objects, because our comparison operator takes an X, and Y is convertible to
X. If you did, you'd be wrong: the comparison operator is only visible to name
lookup if one of the arguments is an X object.
int main(){
A::Y a(1),b(2);
if(a==b) // ERROR: no available comparison operator
do_stuff();
}
If we convert one of the arguments to an X then it works, because the
comparison operator is now visible, and the other argument is converted to an
X to match the function signature:
int main(){
A::Y a(1),b(2);
if(A::X(a)==b) // OK
do_stuff();
}
Similarly, if we declare the comparison operator at namespace scope, everything
works too:
namespace A{
bool operator==(X const& lhs,X const& rhs);
}
int main(){
A::Y a(1),b(2);
if(a==b) // OK now
do_stuff();
}
In this case, the arguments are of type Y, so namespace A is searched, which
now includes the declaration of the comparison operator, so it is found, and the
arguments are converted to X objects to do the comparison.
If we omit this namespace scope definition, as in the original example, then
this function is a hidden friend.
This isn't just limited to operators: normal functions can be defined in
friend declarations too, and just as with the comparison operator above, if
they are not also declared at namespace scope then they are hidden from normal
name lookup. For example:
struct X{
X(int){}
friend void foo(X){};
};
int main(){
X x(42);
foo(x); // OK, calls foo defined in friend declaration
foo(99); // Error: foo not found, as int is not X
::foo(x); // Error: foo not found as ADL not triggered
}
Benefits of Hidden Friends
The first benefit of hidden friends is that it avoids accidental implicit
conversions. In our example above, comparing Y objects doesn't implicitly
convert them to X objects to use the X comparison unless you explicitly do
something to trigger that behaviour. This can avoid accidental uses of the wrong
function too: if I have a function wibble that takes an X and wobble that
takes a Y, then a typo in the function name won't trigger the implicit
conversion to X:
class X{
friend void wibble(X const&){}
};
class Y{
friend void wobble(Y const&){}
public:
operator X() const;
};
int main(){
Y y;
wibble(y); // Error no function wibble(Y)
}
This also helps spot errors where the typo was on the definition: we meant to
define wibble(Y) but misspelled it. With "normal" declarations, the call to
wibble(y) would silently call wibble(X(y)) instead, leading to unexpected
behaviour. Hopefully this would be caught by tests, but it might make it harder
to identify the problem as you'd be checking the definition of wobble,
wondering why it didn't work.
Another consequence is that it makes it easier for the compiler: the hidden
friends are only checked when there is a relevant argument provided. This means
that there are fewer functions to consider for overload resolution, which makes
compilation quicker. This is especially important for operators: if you have a
large codebase, you might have thousands of classes with operator==
defined. If they are declared at namespace scope, then every use of == might
have to check a large number of them and perform overload resolution. If they
are hidden friends, then they are ignored unless one of the expressions being
compared is already of the right type.
In order to truly understand the benefits and use them correctly, we need to
know when hidden friends are visible.
Rules for Visibility of Hidden Friends
Firstly, hidden friends must be functions or function templates; callable
objects don't count.
Secondly, the call site must use an unqualified name — if you use a
qualified name, then that checks only the specified scope, and disregards ADL
(which we need to find hidden friends).
Thirdly, normal unqualified lookup must not find anything that isn't a
function or function template. If you have a local variable int foo;, and try
to call foo(my_object) from the same scope, then the compiler will rightly
complain that this is invalid, even if the type of my_object has a hidden
friend named foo.
Finally, one of the arguments to the function call must be of a user-defined
type, or a pointer or reference to that type.
We now have the circumstances for calling a hidden friend if there is one:
my_object x;
my_object* px=&x;
foo(x);
foo(px);
Both calls to foo in this code will trigger ADL, and search for hidden
friends.
ADL searches a set of namespaces that depend on the type of my_object, but
that doesn't really matter for now, as you could get to normal definitions of
foo in those namespaces by using appropriate qualification. Consider this code:
std::string x,y;
swap(x,y);
ADL will find std::swap, since std::string is in the std namespace, but we
could just as well have spelled out std::swap in the first place. Though this
is certainly useful, it isn't what we're looking at right now.
The hidden friend part of ADL is that for every argument to the function call,
the compiler builds a set of classes to search for hidden friend
declarations. This lookup list is built as follows from a source type list,
which is initially the types of the arguments supplied to the function call.
Our lookup list starts empty. For each type in the source type list:
- If the type being considered is a pointer or reference, add the pointed-to or
referenced type to the source type list
- Otherwise, if the type being considered is a built-in type, do nothing
- Otherwise, if the type is a class type then add it to the lookup list, and
check the following:
- If the type has any direct or indirect base classes, add them to the
lookup list
- If the type is a member of a class, add the containing class to the
lookup list
- If the type is a specialization of a class template, then:
- add the types of any template type arguments (not non-type arguments or
template template arguments) to the source type list
- if any of the template parameters are template template parameters, and
the supplied arguments are member templates, then add the classes of which
those templates are members to the lookup list
- Otherwise, if the type is an enumerated type that is a member of a class, add
that class to the lookup list
- Otherwise, if the type is a function type, add the types of the function
return value and function parameters to the source type list
- Otherwise, if the type is a pointer to a member of some class
X, add the
class X and the type of the member to the source type list
This gets us a final lookup list which may be empty (e.g. in foo(42)), or
may contain a number of classes. All the classes in that lookup list are now
searched for hidden friends. Normal overload resolution is used to determine
which function call is the best match amongst all the found hidden friends, and
all the "normal" namespace-scope functions.
This means that you can add free functions and operators that work on a
user-defined type by adding normal namespace-scope functions, or by adding
hidden friends to any of the classes in the lookup list for that type.
Adding hidden friends via base classes
In a recent blog post, I mentioned
my
strong_typedef implementation. The
initial design for that used an enum class to specify the permitted
operations, but this was rather restrictive, so after talking with some others
(notably Peter Sommerlad) about alternative implementation strategies, I
switched it to a mixin-based implementation. In this case, the Properties
argument is now a variadic parameter pack, which specifies types that provide
mixin classes for the typedef. jss::strong_typedef<Tag,Underlying,Prop>
then derives from
Prop::mixin<jss::strong_typedef<Tag,Underlying,Prop>,Underlying>. This means
that the class template Prop::mixin can provide hidden friends that operate on
the typedef type, but are not considered for "normal" lookup. Consider, for
example, the implementation of
jss::strong_typedef_properties::post_incrementable:
struct post_incrementable {
template <typename Derived, typename ValueType> struct mixin {
friend Derived operator++(Derived &self, int) noexcept(
noexcept(std::declval<ValueType &>()++)) {
return Derived{self.underlying_value()++};
}
};
};
This provides an implementation of operator++ which operates on the strong
typedef type Derived, but is only visible as a hidden friend, so if you do
x++, and x is not a strong typedef that specifies it is post_incrementable
then this operator is not considered, and you don't get accidental conversions.
This makes the strong typedef system easily extensible: you can add new property
types that define mixin templates to provide both member functions and free
functions that operate on the typedef, without making these functions generally
visible at namespace scope.
Hidden Friends and Enumerations
I had forgotten that enumerated types declared inside a class also triggered
searching that class for hidden friends until I was trying to solve a problem
for a client recently. We had some enumerated types that were being used for a
particular purpose, which we therefore wanted to enable operations on that
wouldn't be enabled for "normal" enumerated types.
One option was to specialize a global template as I described in my article
on
Using Enum Classes as Bitfields,
but this makes it inconvenient to deal with enumerated types that are members of
a class (especially if they are private members), and impossible to deal with
enumerated types that are declared at local scope. We also wanted to be able to
declare these enums with a macro, which would mean we couldn't use the
specialization as you can only declare specializations in the namespace in which
the original template is declared, and the macro wouldn't know how to switch
namespaces, and wouldn't be usable at class scope.
This is where hidden friends came to the rescue. You can define a class anywhere
you can define an enumerated type, and hidden friends declared in the enclosing
class of an enumerated type are considered when calling functions that take the
enumerated as a parameter. We could therefore declare our enumerated types with
a wrapper class, like so:
struct my_enum_wrapper{
enum class my_enum{
// enumerations
};
};
using my_enum=my_enum_wrapper::my_enum;
The using declaration means that other code can just use my_enum directly
without having to know or care about my_enum_wrapper.
Now we can add our special functions, starting with a function to verify this is
one of our special enums:
namespace xyz{
constexpr bool is_special_enum(void*) noexcept{
return false;
}
template<typename T>
constexpr bool is_special_enum() noexcept{
return is_special_enum((T*)nullptr);
}
}
Now we can say xyz::is_special_enum<T>() to check if something is one of our
special enumerated types. By default this will call the void* overload, and
thus return false. However, the internal call passes a pointer-to-T as the
argument, which invokes ADL, and searches hidden friends. We can therefore add a
friend declaration to our wrapper class which will be found by ADL:
struct my_enum_wrapper{
enum class my_enum{
// enumerations
};
constexpr bool is_special_enum(my_enum*) noexcept
{
return true;
}
};
using my_enum=my_enum_wrapper::my_enum;
Now, xyz::is_special_enum<my_enum>() will return true. Since this is a
constexpr function, it can be used in a constant expression, so can be used
with std::enable_if to permit operations only for our special enumerated
types, or as a template parameter to specialize a template just for our
enumerated types. Of course, some additional operations can also be added as
hidden friends in the wrapper class.
Our wrapper macro now looks like this:
#define DECLARE_SPECIAL_ENUM(enum_name,underlying_type,...)\
struct enum_name##_wrapper{\
enum class enum_name: underlying_type{\
__VA_ARGS__\
};\
constexpr bool is_special_enum(enum_name*) noexcept\
{\
return true;\
}\
};\
using enum_name=enum_name##_wrapper::enum_name;
so you can declare a special enum as
DECLARE_SPECIAL_ENUM(my_enum,int,a,b,c=42,d). This works at namespace scope,
as a class member, and at local scope, all due to the hidden friend.
Summary
Hidden Friends are a great way to add operations to a specific type without
permitting accidental implicit conversions, or slowing down the compiler by
introducing overloads that it has to consider in other contexts. They also allow
declaring operations on types in contexts that otherwise you wouldn't be able to
do so. Every C++ programmer should know how to use them, so they can be used
where appropriate.
Posted by Anthony Williams
[/ cplusplus /] permanent link
Tags: cplusplus, friends
Stumble It!  | Submit to Reddit
| Submit to Reddit  | Submit to DZone
| Submit to DZone 
Comment on this post
Follow me on Twitter

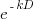 , while hyperbolic discounting has the form
, while hyperbolic discounting has the form  , where:
, where:  is a constant, and
is a constant, and  the period of time.
the period of time.