Derek Jones from The Shape of Code
Moore’s law was a socially constructed project that depended on the coordinated actions of many independent companies and groups of individuals to last for as long it did.
All products evolve, but what was it about Moore’s law that enabled microelectronics to evolve so much faster and for longer than most other products?
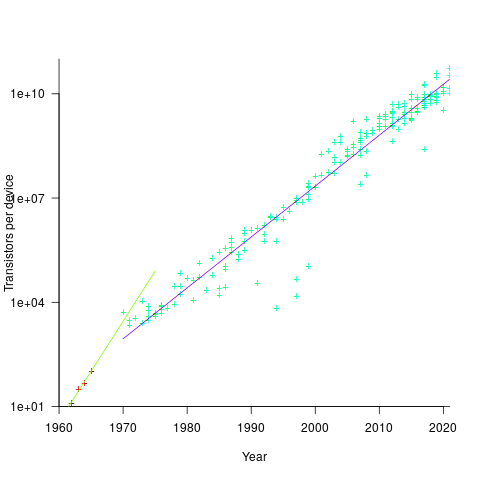
Moore’s observation, made in 1965 based on four data points, was that the number of components contained in a fabricated silicon device doubles every year. The paper didn’t make this claim in words, but a line fitted to four yearly data points (starting in 1962) suggested this behavior continuing into the mid-1970s. The introduction of IBM’s Personal Computer, in 1981 containing Intel’s 8088 processor, led to interested parties coming together to create a hugely profitable ecosystem that depended on the continuance of Moore’s law.
The plot below shows Moore’s four points (red) and fitted regression model (green line). In practice, since 1970, fitting a regression model (purple line) to the number of transistors in various microprocessors (blue/green, data from Wikipedia), finds that the number of transistors doubled every two years (code+data):
In the early days, designing a device was mostly a manual operation; that is, the circuit design and logic design down to the transistor level were hand-drawn. This meant that creating a device containing twice as many transistors required twice as many engineers. At some point the doubling process either becomes uneconomic or it takes forever to get anything done because of the coordination effort.
The problem of needing an exponentially-growing number of engineers was solved by creating electronic design automation tools (EDA), starting in the 1980s, with successive generations of tools handling ever higher levels of abstraction, and human designers focusing on the upper levels.
The use of EDA provides a benefit to manufacturers (who can design differentiated products) and to customers (e.g., products containing more functionality).
If EDA had not solved the problem of exponential growth in engineers, Moore’s law would have maxed-out in the early 1980s, with around 150K transistors per device. However, this would not have stopped the ongoing shrinking of transistors; two economic factors independently incentivize the creation of ever smaller transistors.
When wafer fabrication technology improvements make it possible to double the number of transistors on a silicon wafer, then around twice as many devices can be produced (assuming unchanged number of transistors per device, and other technical details). The wafer fabrication cost is greater (second row in table below), but a lot less than twice as much, so the manufacturing cost per device is much lower (third row in table).
The doubling of transistors primarily provides a manufacturer benefit.
The following table gives estimates for various chip foundry economic factors, in dollars (taken from the report: AI Chips: What They Are and Why They Matter). Node, expressed in nanometers, used to directly correspond to the length of a particular feature created during the fabrication process; these days it does not correspond to the size of any specific feature and is essentially just a name applied to a particular generation of chips.
Node (nm) 90 65 40 28 20 16/12 10 7 5
Foundry sale price per wafer 1,650 1,937 2,274 2,891 3,677 3,984 5,992 9,346 16,988
Foundry sale price per chip 2,433 1,428 713 453 399 331 274 233 238
Mass production year 2004 2006 2009 2011 2014 2015 2017 2018 2020
Quarter Q4 Q4 Q1 Q4 Q3 Q3 Q2 Q3 Q1
Capital investment per wafer 4,649 5,456 6,404 8,144 10,356 11,220 13,169 14,267 16,746
processed per year
Capital consumed per wafer 411 483 567 721 917 993 1,494 2,330 4,235
processed in 2020
Other costs and markup 1,293 1,454 1,707 2,171 2,760 2,990 4,498 7,016 12,753
per wafer
The second economic factor incentivizing the creation of smaller transistors is Dennard scaling, a rarely heard technical term named after the first author of a 1974 paper showing that transistor power consumption scaled with area (for very small transistors). Halving the area occupied by a transistor, halves the power consumed, at the same frequency.
The maximum clock-frequency of a microprocessor is limited by the amount of heat it can dissipate; the heat produced is proportional to the power consumed, which is approximately proportional to the clock-frequency. Instead of a device having smaller transistors consume less power, they could consume the same power at double the frequency.
Dennard scaling primarily provides a customer benefit.
Figuring out how to further shrink the size of transistors requires an investment in research, followed by designing/(building or purchasing) new equipment. Why would a company, who had invested in researching and building their current manufacturing capability, be willing to invest in making it obsolete?
The fear of losing market share is a commercial imperative experienced by all leading companies. In the microprocessor market, the first company to halve the size of a transistor would be able to produce twice as many microprocessors (at a lower cost) running twice as fast as the existing products. They could (and did) charge more for the latest, faster product, even though it cost them less than the previous version to manufacture.
Building cheaper, faster products is a means to an end; that end is receiving a decent return on the investment made. How large is the market for new microprocessors and how large an investment is required to build the next generation of products?
Rock’s law says that the cost of a chip fabrication plant doubles every four years (the per wafer price in the table above is increasing at a slower rate). Gambling hundreds of millions of dollars, later billions of dollars, on a next generation fabrication plant has always been a high risk/high reward investment.
The sales of microprocessors are dependent on the sale of computers that contain them, and people buy computers to enable them to use software. Microprocessor manufacturers thus have to both convince computer manufacturers to use their chip (without breaking antitrust laws) and convince software companies to create products that run on a particular processor.
The introduction of the IBM PC kick-started the personal computer market, with Wintel (the partnership between Microsoft and Intel) dominating software developer and end-user mindshare of the PC compatible market (in no small part due to the billions these two companies spent on advertising).
An effective technique for increasing the volume of microprocessors sold is to shorten the usable lifetime of the computer potential customers currently own. Customers buy computers to run software, and when new versions of software can only effectively be used in a computer containing more memory or on a new microprocessor which supports functionality not supported by earlier processors, then a new computer is needed. By obsoleting older products soon after newer products become available, companies are able to evolve an existing customer base to one where the new product is looked upon as the norm. Customers are force marched into the future.
The plot below shows sales volume, in gigabytes, of various sized DRAM chips over time. The simple story of exponential growth in sales volume (plus signs) hides the more complicated story of the rise and fall of succeeding generations of memory chips (code+data):
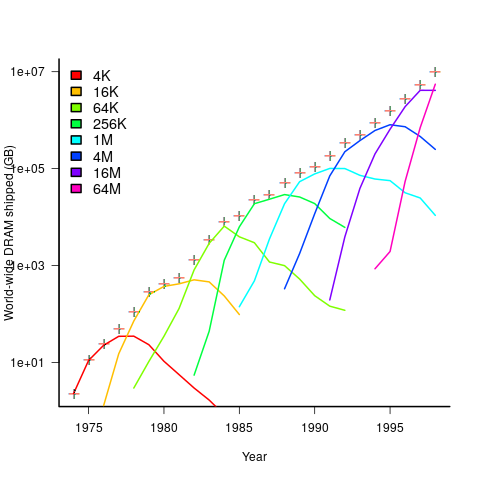
The Red Queens had a simple task, keep buying the latest products. The activities of the companies supplying the specialist equipment needed to build a chip fabrication plant has to be coordinated, a role filled by the International Technology Roadmap for Semiconductors (ITRS). The annual ITRS reports contain detailed specifications of the expected performance of the subsystems involved in the fabrication process.
Moore’s law is now dead, in that transistor doubling now takes longer than two years. Would transistor doubling time have taken longer than two years, or slowed down earlier, if:
- the ecosystem had not been dominated by two symbiotic companies, or did network effects make it inevitable that there would be two symbiotic companies,
- the Internet had happened at a different time,
- if software applications had quickly reached a good enough state,
- if cloud computing had gone mainstream much earlier.
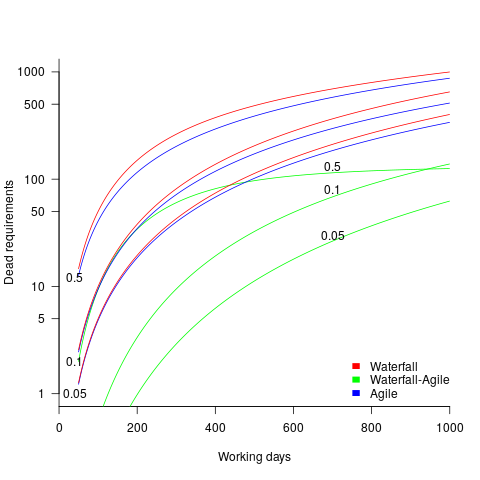
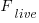 is the fraction of requirements per day that remain relevant to customers. This value is likely to be very close to one, e.g.,
is the fraction of requirements per day that remain relevant to customers. This value is likely to be very close to one, e.g., 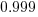 .
.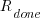 requirements implemented per working day.
requirements implemented per working day.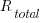 requirements takes
requirements takes 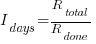 days, and the number of implemented ‘dead’ requirements is (assuming that the no ‘dead’ requirements were present at the end of the requirements gathering phase):
days, and the number of implemented ‘dead’ requirements is (assuming that the no ‘dead’ requirements were present at the end of the requirements gathering phase):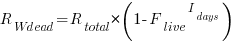
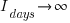 effectively all implemented requirements are ‘dead’.
effectively all implemented requirements are ‘dead’. is given by:
is given by: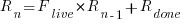
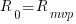 .
. :
: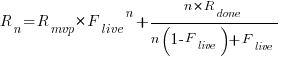
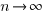 ,
, 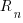 approaches to its maximum value of
approaches to its maximum value of 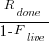
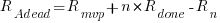
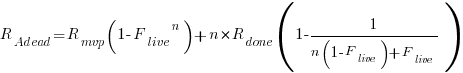
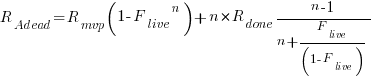
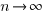 effectively all implemented requirements are ‘dead’, because the number of ‘live’ requirements cannot exceed a known maximum.
effectively all implemented requirements are ‘dead’, because the number of ‘live’ requirements cannot exceed a known maximum.
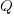 (the derivation assumes that the average quantity in stock is
(the derivation assumes that the average quantity in stock is 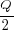 ), it is given by:
), it is given by: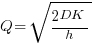 , where
, where 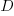 is the quantity consumed per year,
is the quantity consumed per year, 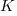 is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods),
is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods), 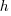 is the annual holding cost per item.
is the annual holding cost per item.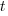 seconds to decide whether a given item should be implemented next, and
seconds to decide whether a given item should be implemented next, and 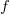 is the fraction of items scanned before one is selected: the average decision time per item is:
is the fraction of items scanned before one is selected: the average decision time per item is: 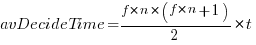 seconds. For example, if
seconds. For example, if 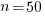 , pulling some numbers out of the air,
, pulling some numbers out of the air, 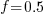 , and
, and 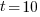 , then
, then 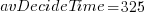 , or 5.4 minutes.
, or 5.4 minutes.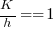 , then
, then 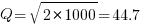 .
.
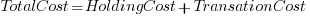 .
. , to reduce the complexity,
, to reduce the complexity,  , of a software system?
, of a software system?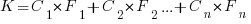
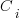 is the system complexity when feature
is the system complexity when feature 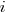 is added, and
is added, and 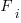 is the cost of adding this feature if no complexity is present.
is the cost of adding this feature if no complexity is present.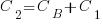 ,
, 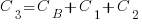 , …
, … 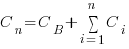
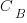 is the base complexity before adding any new features.
is the base complexity before adding any new features.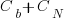 (with
(with 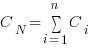 ) to
) to 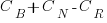 , where
, where 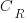 is the reduction in the complexity achieved. The minimum condition for this investment to be worthwhile is that:
is the reduction in the complexity achieved. The minimum condition for this investment to be worthwhile is that: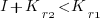 or
or 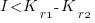
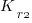 is the total cost of adding new features to the source code after the investment, and
is the total cost of adding new features to the source code after the investment, and 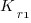 is the total cost of adding the same new features to the source code as it existed immediately prior to the investment.
is the total cost of adding the same new features to the source code as it existed immediately prior to the investment.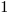 , we have:
, we have: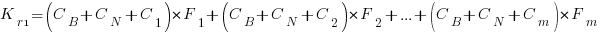
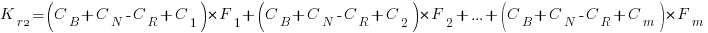
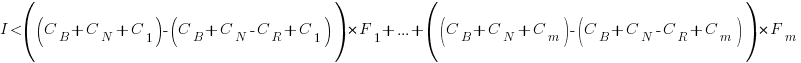
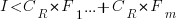
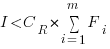
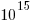 ). The
). The 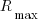 (based on benchmark performance, i.e.,
(based on benchmark performance, i.e.,  (what the hardware is theoretically capable of, which is sometimes more than twice
(what the hardware is theoretically capable of, which is sometimes more than twice 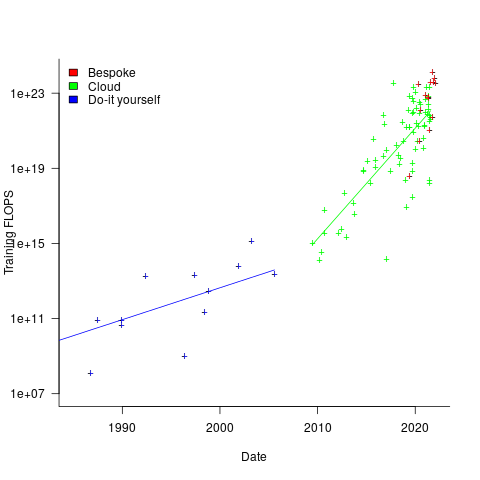
 and
and  parameters, which I assume is the result of bespoke systems having the memory capacity to handle more parameters (
parameters, which I assume is the result of bespoke systems having the memory capacity to handle more parameters (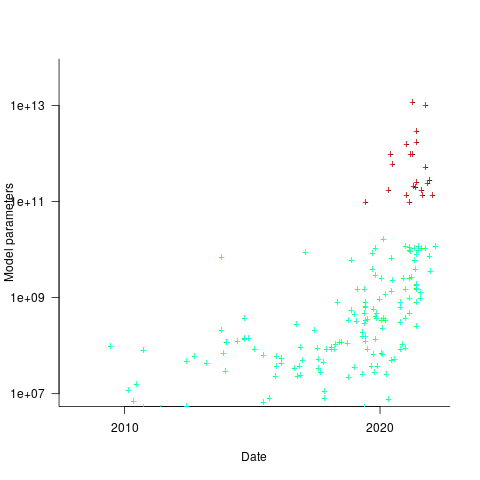
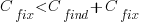 .
.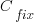 is the cost of fixing the mistake in the code (including testing etc), and
is the cost of fixing the mistake in the code (including testing etc), and 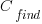 is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).
is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).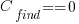 , e.g., a developer reading the code for another reason, or flagged by a static analysis tool.
, e.g., a developer reading the code for another reason, or flagged by a static analysis tool.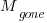 be the likelihood that the coding mistake ceases to exist in the next unit of time.
be the likelihood that the coding mistake ceases to exist in the next unit of time.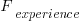 be the likelihood that a fault is reported in the next time unit.
be the likelihood that a fault is reported in the next time unit.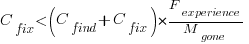
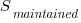 , is slightly less than one.
, is slightly less than one.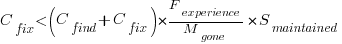
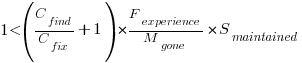
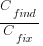 ?
?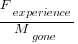 are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of
are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of 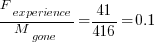
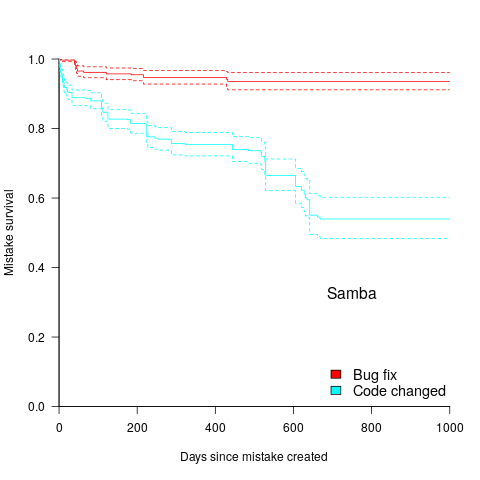
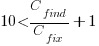 .
.

 , blue line is a fitted
, blue line is a fitted