Posted on

Over/under estimation factor for ‘most estimates’

Derek Jones from The Shape of Code

When asked to estimate the time taken to perform a software development related task, people regularly over or under estimate. What range of over/under estimation falls within the bounds of the term ‘most estimates’, i.e., the upper/lower bounds of the ratio 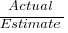Actual/Estimate (an overestimate occurs when 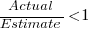Actual/Estimate < 1, an underestimate when 1 < Actual/Estimate)?

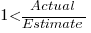On Twitter, I have been citing a factor of two for over/under time estimates. This factor of two involves some assumptions and a personal interpretation.

The following analysis is based on the two major software task effort estimation datasets: SiP and CESAW. The tasks in both datasets are for internal projects (i.e., no tendering against competitors), and require at most a few hours work.

The following analysis is based on the SiP data.

Of the 8,252 unique tasks in the SiP data, 30% are underestimates, 37% exact, and 33% overestimates.

How do we go about calculating bounds for the over/under factor of most estimates (a previous post discussed calculating an accuracy metric over all estimates)?

A simplistic approach is to average over each of the overestimated and underestimated tasks. The plot below shows hours estimated against the ratio actual/estimated, for each task (code+data):

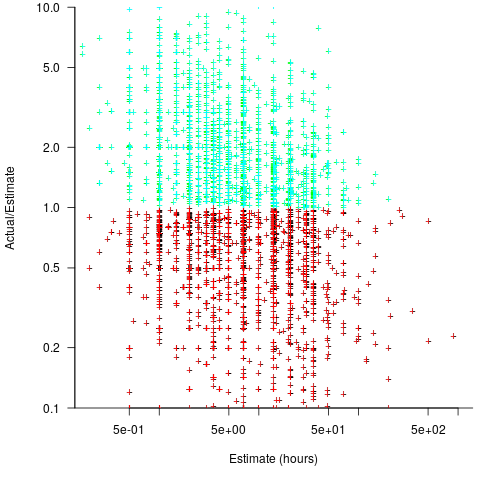
Actual/estimate ratio for SiP tasks having a given Estimate value.

Averaging the over/under estimated tasks separately (using the geometric mean) gives 0.47 and 1.9 respectively, i.e., tasks are over/under estimated by a factor of two.

This approach fails to take into account the number of estimates that are over/under/equal, i.e., it ignores likelihood information.

A regression model takes into account the distribution of values, and we could adopt the fitted model’s prediction interval as the over/under confidence intervals. The prediction interval is the interval within which other observations are expected to fall, with some probability (R’s predict function uses one standard deviation).

The plot below shows a fitted regression model and prediction intervals at one standard deviation (68.3%) and two standard deviations (95%); the faint grey line shows Estimate == Actual (code+data):

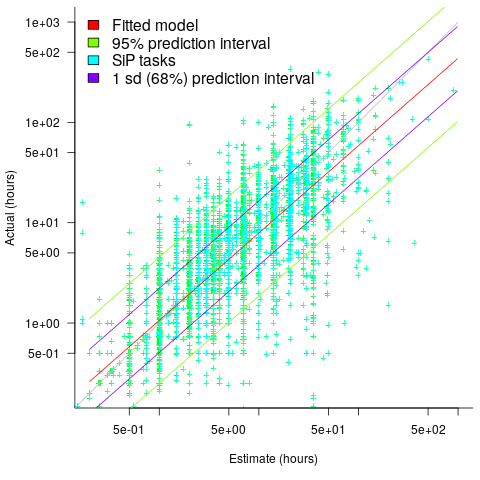
Fitted regression model and prediction intervals at 68.3% and 95%.

The fitted model tilts down from the upward direction of the Estimate == Actual line, consequently the over/under estimation factor depends on the size of the estimate. The table below lists the over/under estimation factor for low/high estimates at one & two standard deviations (68.3 and 95% probability).

People like simple answers (i.e., single values) and the mean value is a commonly used technique of summarising many values. The task estimate values are unevenly distributed and weighting the mean by the distribution of estimated values is more representative than, say, an evenly distributed set of estimates. The 5th and 6th columns in the table below list the weighted means at one/two standard deviations (the CESAW columns are the values for all projects in the CESAW data).

          1 sd           2 sd        Weighted mean       CESAW
       Low    High   Low    High     1 sd    2 sd     1 sd   2 sd
Over   0.56   0.24   0.27   0.11     0.46    0.25     0.29   0.1
Under  2.4    1.0    4.9    2.0      2.00    4.1      2.4    6.5

The weighted means for over/under estimates are close to a factor of two of the actual (divide/multiply) within one standard deviation (68.3%), and a factor of four within two standard deviations (95%).

Why choose to give the one standard deviation factor, rather than the two? People talk of “most estimates”, but what percentage range does ‘most’ map to? I have tended to think of ‘most’ as more than two-thirds, e.g., at least one standard deviation (a recent study suggests that ‘most’ usage peaks at 80-85%), and I think of two standard deviations as ‘nearly all’ (i.e., 95%; there are probably people who call this ‘most’).

Perhaps a between two and four is a more appropriate answer (particularly since the bounds are wider for the CESAW data). Suggestions welcome.

Posted on

The CESAW dataset: a brief introduction

Derek Jones from The Shape of Code

I have found that the secret for discovering data treasure troves is persistently following any leads that appear. For instance, if a researcher publishes a data driven paper, then check all their other papers. The paper: Composing Effective Software Security Assurance Workflows contains a lot of graphs and tables, but no links to data, however, one of the authors (William R. Nichols) published The Cost and Benefits of Static Analysis During Development which links to an amazing treasure trove of project data.

My first encounter with this data was this time last year, as I was focusing on completing my Evidence-based software engineering book. Apart from a few brief exchanges with Bill Nichols the technical lead member of the team who obtained and originally analysed the data, I did not have time for any detailed analysis. Bill was also busy, and we agreed to wait until the end of the year. Bill’s and my paper: The CESAW dataset: a conversation is now out, and focuses on an analysis of the 61,817 task and 203,621 time facts recorded for the 45 projects in the CESAW dataset.

Our paper is really an introduction to the CESAW dataset; I’m sure there is a lot more to be discovered. Some of the interesting characteristics of the CESAW dataset include:

  • it is the largest publicly available project dataset currently available, with six times as many tasks as the next largest, the SiP dataset. The CESAW dataset involves the kind of data that is usually encountered, i.e., one off project data. The SiP dataset involves the long term evolution of one company’s 20 projects over 10-years,
  • it includes a lot of information I have not seen elsewhere, such as: task interruption time and task stop/start {date/time}s (e.g., waiting on some dependency to become available)
  • four of the largest projects involve safety critical software, for a total of 28,899 tasks (this probably more than two orders of magnitude more than what currently exists). Given all the claims made about the development about safety critical software being different from other kinds of development, here is a resource for checking some of the claims,
  • the tasks to be done, to implement a project, are organized using a work-breakdown structure. WBS is not software specific, and the US Department of Defense require it to be used across all projects; see MIL-STD-881. I will probably annoy those in software management by suggesting the one line definition of WBS as: Agile+structure (WBS supports iteration). This was my first time analyzing WBS project data, and never having used it myself, I was not really sure how to approach the analysis. Hopefully somebody familiar with WBS will extract useful patterns from the data,
  • while software inspections are frequently talked about, public data involving them is rarely available. The WBS process has inspections coming out of its ears, and for some projects inspections of one kind or another represent the majority of tasks,
  • data on the kinds of tasks that are rarely seen in public data, e.g., testing, documentation, and design,
  • the 1,324 defect-facts include information on: the phase where the mistake was made, the phase where it was discovered, and the time taken to fix.

As you can see, there is lots of interesting project data, and I look forward to reading about what people do with it.

Once you have downloaded the data, there are two other sources of information about its structure and contents: the code+data used to produce the plots in the paper (plus my fishing expedition code), and a CESAW channel on the Evidence-based software engineering Slack channel (no guarantees about response time).