Derek Jones from The Shape of Code
On multi-person projects people have to talk to each other, which reduces the amount of time available for directly working on writing software. How many people can be added to a project before the extra communications overhead is such that the total amount of code, per unit time, produced by the team decreases?
A rarely cited paper by Robert Tausworthe provides a simple, but effective analysis.
Activities are split between communicating and producing code.
If we assume the communications overhead is give by: 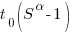 , where
, where  is the percentage of one person’s time spent communicating in a two-person team,
is the percentage of one person’s time spent communicating in a two-person team,  the number of developers and
the number of developers and  a constant greater than zero (I’m using Tausworthe’s notation).
a constant greater than zero (I’m using Tausworthe’s notation).
The maximum team size, before adding people reduces total output, is given by: 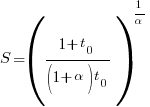 .
.
If  (i.e., everybody on the project has the same communications overhead), then
(i.e., everybody on the project has the same communications overhead), then  , which for small
, which for small  is approximately
is approximately  . For example, if everybody on a team spends 10% of their time communicating with every other team member:
. For example, if everybody on a team spends 10% of their time communicating with every other team member:  .
.
In this team of five, 50% of each persons time will be spent communicating.
If  , then we have
, then we have 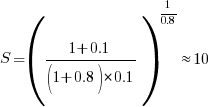 .
.
What if the percentage of time a person spends communicating with other team members has an exponential distribution? That is, they spend most of their time communicating with a few people and very little with the rest; the (normalised) communications overhead is:  , where
, where  is a constant found by fitting data from the two-person team (before any more people are added to the team).
is a constant found by fitting data from the two-person team (before any more people are added to the team).
The maximum team size is now given by:  , and if
, and if  , then:
, then:  .
.
In this team of ten, 63% of each persons time will be spent communicating (team size can be bigger, but each member will spend more time communicating compared to the linear overhead case).
Having done this analysis, what is now needed is some data on the distribution of individual communications overhead. Is the distribution linear, square-root, exponential? I am not aware of any such data (there is a chance I have encountered something close and not appreciated its importance).
I have only every worked on relatively small teams, and am inclined towards the distribution of time spent communicating not being constant. Was it exponential or a power-law? I would not like to say.
Could a communications time distribution be reverse engineered from email logs? The cc’ing of people who might have an interest in a topic complicates the data analysis; time spent in meetings are another complication.
Pointers to data most welcome and as is any alternative analysis using data likely to have a higher signal/noise ratio.
