Derek Jones from The Shape of Code
Projects that use Scrum as their project management framework estimate tasks (known as a user story, or just story) in units of Story-points. A collection of User stories are grouped together to be implemented during a Sprint (a time-boxed interval, often lasting 2-weeks).
What are Story-points, and how do they map to time (in hours and minutes)? For this post, let’s ignore these questions, simply assuming that the people who assign a story-point value to a story have some mapping in their head.
What is the average number of story-points in a story, and how does this average vary across teams? What is the distribution of number of stories estimated per sprint, how many are actually implemented, and how does this vary across teams?
The data required to answer these questions has not been publicly available, or rather public data is not known to me. Until this week, I had only known of a few public Jira repos where story-points were given for at most a few hundred stories.
The LSST Corporation, a not-for-profit involved in astronomy and physics research, has a Data Management (DM) project. The Jira repo for this project contains 26,671 ‘Done’ issues (as of Aug 2022), of which 11,082 (41.5%) have assigned story-points; there have been 469 sprints, which involved 33% of the issues. The start/end implementation date/time for stories is mostly rather granular, and not fine enough to be used to attempt to correlate individual stories with hours. I found this repo, and a couple of others, via the paper Story points changes in agile iterative development, and downloaded all available issues.
What patterns are present in the story-point and sprint data?
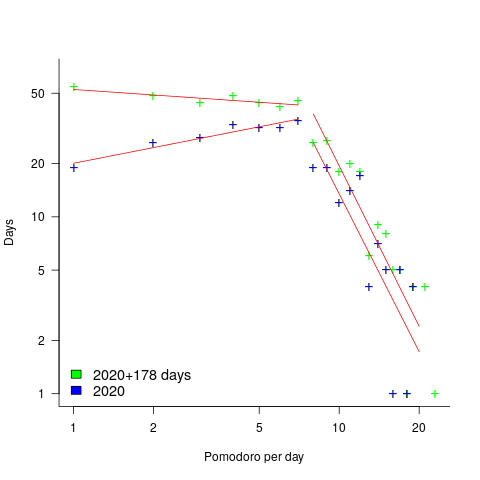
Story points are commonly thought of as being integer valued, but 28% of the values are non-integer. If any developers are using the Fibonacci scale, there are not enough to have a noticeable impact. The plot below shows the number of stories estimated to involve a given number of story-points (black pluses are non-integer values, which have been rounded to fit the regression model). The green curved line is a fitted biexponential (sum of two exponentials), with the two straight lines being the two component exponentials (code+data):
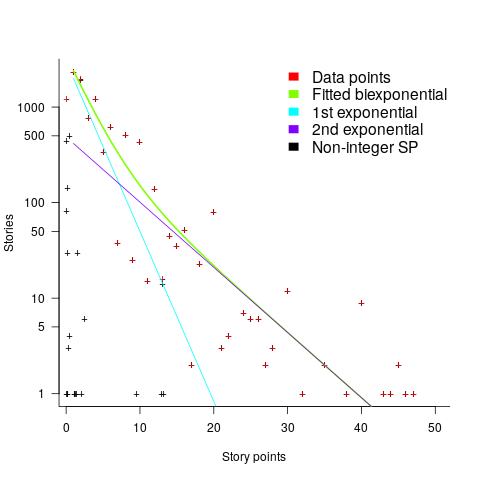
One exponential is dominant for stories assigned up to 10 story-points, and the second exponential for higher story-point values.
The development team decides to implement a story and allocates it to a sprint. A story may be reallocated to another sprint before the start of the original sprint, or after the sprint is finished when its implementation is incomplete or not yet started (the data does not allow for these cases to be distinguished). How many sprints is a story allocated to, before the story implementation is complete?
The plot below shows the number of stories allocated to a given number of sprints, with a fitted regression line of the form 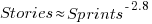 (code+data):
(code+data):
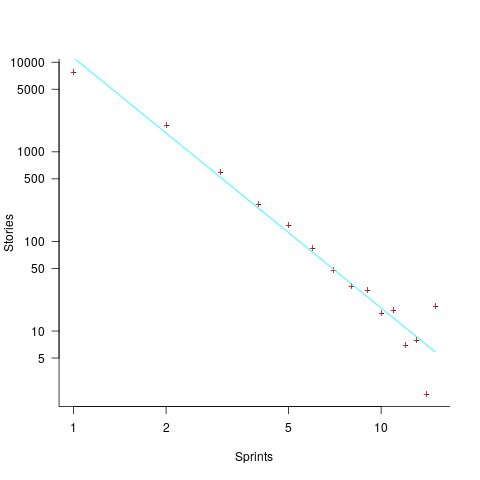
So around 14% of stories are allocated to two sprints, 5% to three and 2% to four.
How many stories are assigned to a sprint? The plot below shows the number of sprints having a given number of stories assigned to them, and the number of sprints implementing a given number of stories; lines are fitted loess models (code+data):
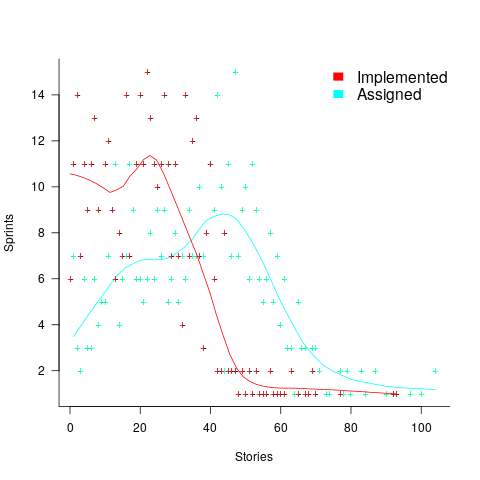
Are the Story/Story-point/Sprint patterns found in the DM project likely to occur in other projects using Scrum?
I don’t know, but I hope so. Developing theories of software development processes requires that there be consistent patterns of behavior.
Not knowing what stories were assigned to a sprint at the start of the sprint, rather assigned earlier and then moved to another sprint, potentially undermines the sprint patterns. We will have to wait and see.
If anybody knows of any public Jira repos where a high percentage (say 40%) of the issues have been assigned story-points, please let me know (all the ones I know of on the Atlassian site contain a tiny percentage of story-points).

 .
.
 , where:
, where:  is the Pomodoros worked on day
is the Pomodoros worked on day  ,
,  Pomodoros worked on the previous day,
Pomodoros worked on the previous day,  is white noise (e.g., a Normal distribution) with a zero mean and a standard deviation of 4 (in this case) on day
is white noise (e.g., a Normal distribution) with a zero mean and a standard deviation of 4 (in this case) on day  the previous day’s noise (see
the previous day’s noise (see 

![S_{sd-est}=sqrt{f_2 [0.25k^2 ({f_1}/{f_2} )^4+k^2 ({f_1}/{f_2} )^3+0.5k ({f_1}/{f_2} )^2 ]} S_{sd-est}=sqrt{f_2 [0.25k^2 ({f_1}/{f_2} )^4+k^2 ({f_1}/{f_2} )^3+0.5k ({f_1}/{f_2} )^2 ]}](http://shape-of-code.coding-guidelines.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_971.5_9eaa74a0e52ef66cad3146183e24b04f.png)
 is the estimated number of distinct faults,
is the estimated number of distinct faults,  the observed number of distinct faults,
the observed number of distinct faults,  the total number of faults,
the total number of faults,  the number of distinct faults that occurred once,
the number of distinct faults that occurred once,  the number of distinct faults that occurred twice,
the number of distinct faults that occurred twice,  .
.