Derek Jones from The Shape of Code
What are the rules for deciding when two types are the same, or compatibility?
This question needs to be answered to decide whether an object of type T1 can be assigned to an object of type T2, whether they can be compared, added together, etc.
A wide collection of rules have been combined together, by various languages, for type compatibility of scalar types (e.g., integer, character, etc), but for aggregate types two rules dominate: name equivalence, and structural equivalence, or some combination.
With name equivalence, two types are the same if they are declared using the same name (e.g., the name of the tag for a union type, in C)
With structural equivalence, two types are compatible if they have a compatible structure, i.e., their internal contents are type compatible (this requires walking over each field/member checking that it is compatible). For instance, an object declared to have an aggregate type containing three integers is compatible with another aggregate type containing three integers (assuming any type modifiers, such as const’ness or mutability, are the same).
Structural compatibility becomes interesting when pointer types are involved; the pointed to types need to be checked and loops can occur, e.g., type S1 contains a field that has a type pointer to S2, which contains a field that has type pointer to S1.
While most types are easily checked for structural compatibility, every now and again aggregate types connect together in a way that makes it non-trivial to figure out which types are structurally compatible (dot file; needs graphviz):
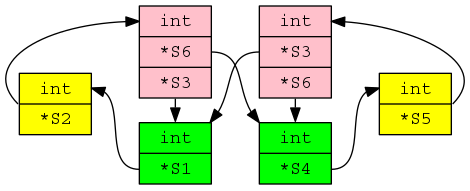
Handling the edge cases requires maintaining a stack of information about which pairs of types are currently being compared.
In C, type compatibility is a combination of name equivalence (for aggregate types in the same translation unit) and structural equivalence (for function types and aggregate types across translation units).
Function types have to use structural equivalence because the type in a function definition is anonymous (the function name that appears in the definition has this anonymous type), there is no name to compare.
Cycles cannot appear in function types (in C), because the identifier being defined in a typedef is not in scope until just after the completion of its declarator. It is not possible to refer to the identifier being defined insider its own definition (e.g., it is not possible to define a function that takes its own type as a parameter; in typedef int (*f)(f); the second f is a redundant parameter name, the scope of the type denoted by the first f begins just before the semicolon).
Structural equivalence across translation units is a hangover from the early days of C, when developers were sloppy when using (or not) tag names (with different people having different rules for using upper/lower case tag names); developers’ knew what the layout in memory was and created the necessary types for their use of this data.
Type compatibility via name equivalence is easy to explain and makes it explicit when developers are bending the rules (i.e., pointer to struct casts appear in the code).
Type compatibility via structural equivalence is the wild west, which still exists in some development environments.
