Derek Jones from The Shape of Code
Predicting the peak of data fitted by a logistic equation is attracting a lot of attention at the moment. Let’s see how well we can predict the final size of a software system, in lines of code, using logistic regression (code+data).
First up is the size of the GNU C library. This is not really a good test, since the peak (or rather a peak) has been reached.
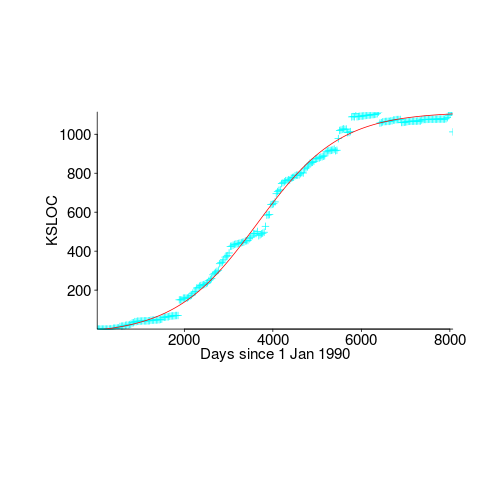
We need a system that has not yet reached an easily recognizable peak. The Linux kernel has been under development for many years, and lots of LOC counts are available. The plot below shows a logistic equation fitted to the kernel data, assuming that the only available data was up to day: 2,900, 3,650, 4,200, and 5,000+. Can you tell which fitted line corresponds to which number of days?
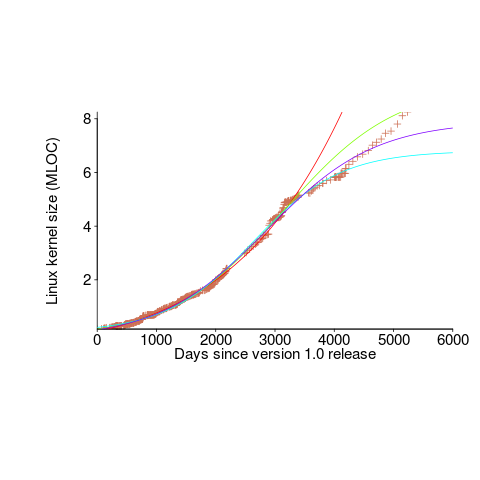
The underlying ‘problem’ is that we are telling the fitting software to fit a particular equation; the software does what it has been told to do, and fits a logistic equation (in this case).
A cubic polynomial is also a great fit to the existing kernel data (red line to the left of the blue line), and this fitted equation can be extended into future (to the right of the blue line); dotted lines are 95% confidence bounds. Do any readers believe the future size of the Linux kernel predicted by this cubic model?
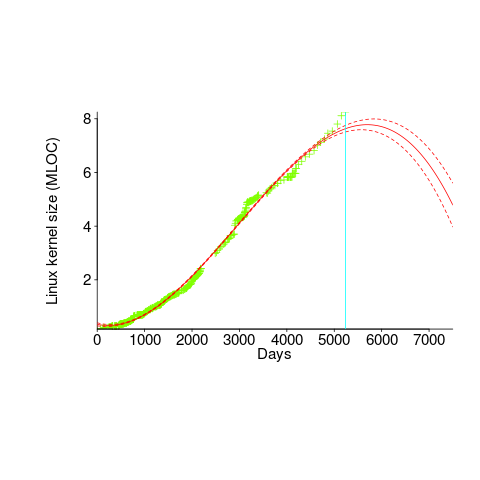
Predicting the future requires lots of data on the underlying processes that drive events. Modeling events is an iterative process. Build a model, check against reality, adjust model, rinse and repeat.
If the COVID-19 experience trains people to be suspicious of future predictions made by models, it will have done something positive.
