Derek Jones from The Shape of Code
Tracking down coding mistakes is a common developer activity (for which training is rarely provided).
Debugging code involves reasoning about differences between the actual and expected output produced by particular program input. The goal is to figure out the coding mistake, or at least narrow down the portion of code likely to contain the mistake.
Interest in human reasoning dates back to at least ancient Greece, e.g., Aristotle and his syllogisms. The study of the psychology of reasoning is very recent; the field was essentially kick-started in 1966 by the surprising results of the Wason selection task.
Debugging involves a form of deductive reasoning known as conditional reasoning. The simplest form of conditional reasoning involves an input that can take one of two states, along with an output that can take one of two states. Using coding notation, this might be written as:
if (p) then q if (p) then !q
if (!p) then q if (!p) then !q
The notation used by the researchers who run these studies is a 2×2 contingency table (or conditional matrix):
OUTPUT
1 0
1 A B
INPUT
0 C D
where: A, B, C, and D are the number of occurrences of each case; in code notation, p is the input and q the output.
The fertilizer-plant problem is an example of the kind of scenario subjects answer questions about in studies. Subjects are told that a horticultural laboratory is testing the effectiveness of 31 fertilizers on the flowering of plants; they are told the number of plants that flowered when given fertilizer (A), the number that did not flower when given fertilizer (B), the number that flowered when not given fertilizer (C), and the number that did not flower when not given any fertilizer (D). They are then asked to evaluate the effectiveness of the fertilizer on plant flowering. After the experiment, subjects are asked about any strategies they used to make judgments.
Needless to say, subjects do not make use of the available information in a way that researchers consider to be optimal, e.g., Allan’s 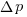 index
index 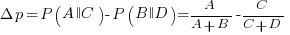 (sorry about the double,
(sorry about the double, 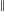 , rather than single, vertical lines).
, rather than single, vertical lines).
What do we know after 40+ years of active research into this basic form of conditional reasoning?
The results consistently find, for this and other problems, that the information A is given more weight than B, which is given by weight than C, which is given more weight than D.
That information provided by A and B is given more weight than C and D is an example of a positive test strategy, a well-known human characteristic.
Various models have been proposed to ‘explain’ the relative ordering of information weighting: 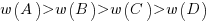 , e.g., that subjects have a bias towards sufficiency information compared to necessary information.
, e.g., that subjects have a bias towards sufficiency information compared to necessary information.
Subjects do not always analyse separate contingency tables in isolation. The term blocking is given to the situation where the predictive strength of one input is influenced by the predictive strength of another input (this process is sometimes known as the cue competition effect). Debugging is an evolutionary process, often involving multiple test inputs. I’m sure readers will be familiar with the situation where the output behavior from one input motivates a misinterpretation of the behaviour produced by a different input.
The use of logical inference is a commonly used approach to the debugging process (my suggestions that a statistical approach may at times be more effective tend to attract odd looks). Early studies of contingency reasoning were dominated by statistical models, with inferential models appearing later.
Debugging also involves causal reasoning, i.e., searching for the coding mistake that is causing the current output to be different from that expected. False beliefs about causal relationships can be a huge waste of developer time, and research on the illusion of causality investigates, among other things, how human interpretation of the information contained in contingency tables can be ‘de-biased’.
The apparently simple problem of human conditional reasoning over two variables, each having two states, has proven to be a surprisingly difficult to model. It is tempting to think that the performance of professional software developers would be closer to the ideal, compared to the typical experimental subject (e.g., psychology undergraduates or Mturk workers), but I’m not sure whether I would put money on it.
