Chris Oldwood from The OldWood Thing
My recent tirade against unnecessary branching – “Git is Not the Problem†– might have given the impression that I don’t appreciate the power that git provides. That’s not true and hopefully the following example highlights the appreciation I have for the power git provides but also why I dislike being put in that position in the first place.
The Branching Strategy
I was working in a small team with a handful of experienced developers making an old C++/ATL based GUI more accessible for users with disabilities. Given the codebase was very mature and maintenance was minimal, our remit only extended so far as making the minimal changes we needed to both the code and resource files. Hence this effectively meant no refactoring – a strictly surgical approach.
The set-up involved an integration branch per-project with us on one and the client’s team on another – master was reserved for releases. However, as they were using Stash for their repos they also wanted us to make use of its ability to create separate pull requests (PR) for every feature. This meant we needed to create independent branches for every single feature as we didn’t have permission to push directly to the integration branch even if we wanted to.
The Bottleneck
For those who haven’t had the pleasure of working with Visual Studio and C++/ATL on a native GUI with other people, there are certain files which tend to be a bottleneck, most notably resource.h. This file contains the mapping for the symbols (nay #defines) to the resource file IDs. Whenever you add a new resource, such as a localizable string, you add a new symbol and bump the two “next ID†counters at the bottom. This project ended up with us adding a lot of new resource strings for the various (localizable) annotations we used to make the various dialog controls more accessible [1].
Aside from the more obvious bottleneck this resource.h file creates, in terms of editing it in a team scenario, it also has one other undesirable effect – project rebuilds. Being a header file, and also one that has a habit of being used across most of the codebase (whether intentionally or not) if it changes then most of the codebase needs re-building. On a GUI of the size we were working on, using the development VMs we had been provided, this amounted to 45 minutes of thumb twiddling every time it changed. As an aside we couldn’t use the built-in Visual Studio editor either as the file had been edited by hand for so long that when it was saved by the editor you ended up with the diff from hell [2].
The Side-Effects
Consequently we ran into two big problems working on this codebase that were essentially linked to that one file. The first was that adding new resources meant updating the file in a way that was undoubtedly going to generate a merge conflict with every other branch because most tasks meant adding new resources. Even though we tried to coordinate ourselves by introducing padding into the file and artificially bumping the IDs we still ended up causing merge conflicts most of the time.
In hindsight we probably could have made this idea work if we added a huge amount of padding up front and reserved a large range of IDs but we knew there was another team adding GUI stuff on another branch and we expected to integrate with them more often than we did. (We had no real contact with them and the plethora of open branches made it difficult to see what code they were touching.)
The second issue was around the rebuilds. While you can git checkout –b <branch> to create your feature branch without touching resource.h again, the moment you git pull the integration branch and merge you’re going to have to take the hit [3]. Once your changes are integrated and you push your feature branch to the git server it does the integration branch merge for you and moves it forward.
Back on your own machine you want to re-sync by switching back to the integration branch, which I’d normally do with:
> git checkout <branch>
> git pull --ff-only
…except the first step restores the old resource.h before updating it again in the second step back to where you just were! Except now we’ve got another 45 minute rebuild on our hands [3].
Git to the Rescue
It had been some years since any of us had used Visual Studio on such a large GUI and therefore it took us a while to work out why the codebase always seemed to want rebuilding so much. Consequently I looked to the Internet to see if there was a way of going from my feature branch back to the integration branch (which should be identical from a working copy perspective) without any files being touched. It’s git, of course there was a way, and “Fast-forwarding a branch without checking it out†provided the answer [4]:
> git fetch origin <branch>:<branch>
> git checkout <branch>
The trick is to fetch the branch changes from upstream and point the local copy of that branch to its tip. Then, when you do checkout, only the branch metadata needs to change as the versions of the files are identical and nothing gets touched (assuming no other upstream changes have occurred in the meantime).
Discontinuous Integration
In a modern software development world where we strive to integrate as frequently as possible with our colleagues it’s issues like these that remind us what some of the barriers are for some teams. Visual C++ has been around a long time (since 1993) so this problem is not new. It is possible to break up a GUI project – it doesn’t need to have a monolithic resource file – but that requires time & effort to fix and needs to be done in a timely fashion to reap the rewards. In a product this old which is effectively on life-support this is never going to happen now.
As Gerry Weinberg once said “Things are the way they are because they got that way†which is little consolation when the clock is ticking and you’re watching the codebase compile, again.
[1] I hope to write up more on this later as the information around this whole area for native apps was pretty sparse and hugely diluted by the same information for web apps.
[2] Luckily it’s a fairly easy format but laying out controls by calculating every window rectangle is pretty tedious. We eventually took a hybrid approach for more complex dialogs where we used the resource editor first, saved our code snippet, reverted all changes, and then manually pasted our snippet back in thereby keeping the diff minimal.
[3] Yes, you can use touch to tweak the file’s timestamp but you need to be sure you can get away with that by working out what the effects might be.
[4] As with any “googling†knowing what the right terms are, to ask the right question, is the majority of the battle.



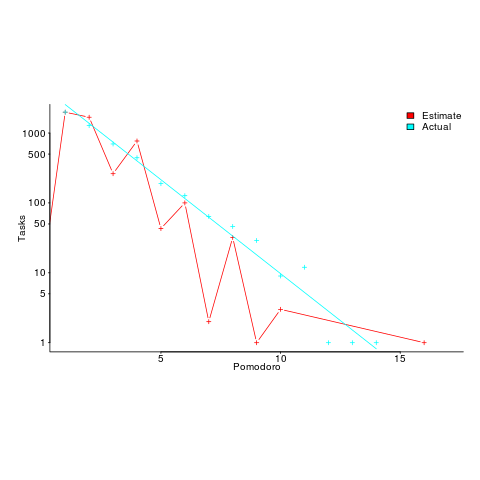
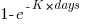 , where:
, where:  is a constant and
is a constant and  is the number of days since the start of the interval fitted. The second (middle) black line is a fitted straight line.
is the number of days since the start of the interval fitted. The second (middle) black line is a fitted straight line.

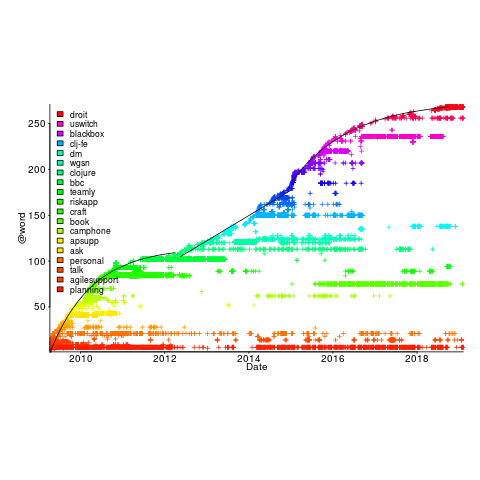
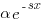 and
and 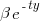 , respectively. The constants
, respectively. The constants  and
and  are needed to ensure that both probabilities sum to one; the exponents
are needed to ensure that both probabilities sum to one; the exponents  and
and  control the distribution of values. What is the probability that
control the distribution of values. What is the probability that  , where:
, where:  is the probability distribution function for
is the probability distribution function for  (in this case:
(in this case: 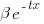 ), and
), and  the the
the the  (in this case:
(in this case:  ).
). .
.