Derek Jones from The Shape of Code
Two years ago, my book Evidence-based Software Engineering: based on the publicly available data was released. The first two weeks saw 0.25 million downloads, and 0.5 million after six months. The paperback version on Amazon has sold perhaps 20 copies.
How have the book contents fared, and how well has my claim to have discussed all the publicly available software engineering data stood up?
The contents have survived almost completely unscathed. This is primarily because reader feedback has been almost non-existent, and I have hardly spent any time rereading it.
In the last two years I have discovered maybe a dozen software engineering datasets that would have been included, had I known about them, and maybe another dozen non-software related datasets that could have been included in the Human behavior/Cognitive capitalism/Ecosystems/Reliability chapters. About half of these have been the subject of blog posts (links below), with the others waiting to be covered.
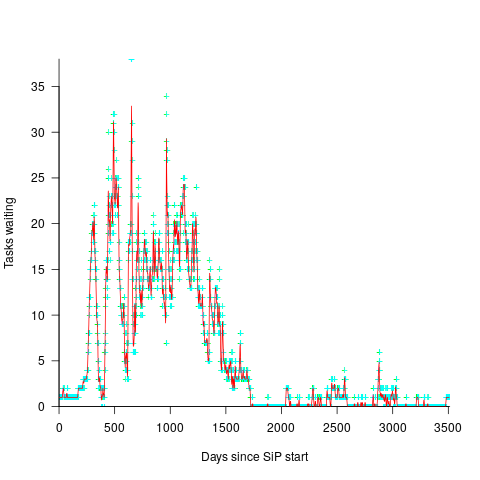
Each dataset provides a sliver of insight into the much larger picture that is software engineering; joining the appropriate dots, by analyzing multiple datasets, can provide a larger sliver of insight into the bigger picture. I have not spent much time attempting to join dots, but have joined a few tiny ones, and a few that are not so small, e.g., Estimating using a granular sequence of values and Task backlog waiting times are power laws.
I spent the first year, after the book came out, working through the backlog of tasks that had built up during the 10-years of writing. The second year was mostly dedicated to trying to find software project data (including joining Twitter), and reading papers at a much reduced rate.
The plot below shows the number of monthly downloads of the A4 and mobile friendly pdfs, along with the average kbytes per download (code+data):
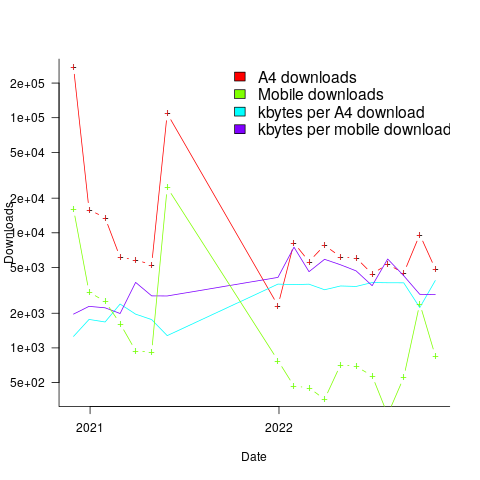
The monthly averages for 2022 are around 6K A4 and 700 mobile friendly pdfs.
I have been averaging one in-person meetup per week in London. Nearly everybody I tell about the book has not previously heard of it.
The following is a list of blog posts either analyzing existing data or discussing/analyzing new data.
Introduction
analysis: Software effort estimation is mostly fake research
analysis: Moore’s law was a socially constructed project
Human behavior
data (reasoning): The impact of believability on reasoning performance
data: The Approximate Number System and software estimating
data (social conformance): How large an impact does social conformity have on estimates?
data (anchoring): Estimating quantities from several hundred to several thousand
data: Cognitive effort, whatever it might be
Ecosystems
data: Growth in number of packages for widely used languages
data: Analysis of a subset of the Linux Counter data
data: Overview of broad US data on IT job hiring/firing and quitting
Projects
analysis: Delphi and group estimation
analysis: The CESAW dataset: a brief introduction
analysis: Parkinson’s law, striving to meet a deadline, or happenstance?
analysis: Evaluating estimation performance
analysis: Complex software makes economic sense
analysis: Cost-effectiveness decision for fixing a known coding mistake
analysis: Optimal sizing of a product backlog
analysis: Evolution of the DORA metrics
analysis: Two failed software development projects in the High Court
data: Pomodoros worked during a day: an analysis of Alex’s data
data: Multi-state survival modeling of a Jira issues snapshot
data: Over/under estimation factor for ‘most estimates’
data: Estimation accuracy in the (building|road) construction industry
data: Rounding and heaping in non-software estimates
data: Patterns in the LSST:DM Sprint/Story-point/Story ‘done’ issues
data: Shopper estimates of the total value of items in their basket
Reliability
analysis: Most percentages are more than half
Statistical techniques
Fitting discontinuous data from disparate sources
Testing rounded data for a circular uniform distribution
Post 2020 data
Pomodoros worked during a day: an analysis of Alex’s data
Impact of number of files on number of review comments
Finding patterns in construction project drawing creation dates

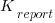 (there was an incentive to report higher/lower, and punishment for being caught being inaccurate). The Receiver could accept or reject the number of red balls reported by the Sender. In the actual experiment, unknown to the human subjects, one of every game’s subject pair was always played by a computer. Every subject played 100 games.
(there was an incentive to report higher/lower, and punishment for being caught being inaccurate). The Receiver could accept or reject the number of red balls reported by the Sender. In the actual experiment, unknown to the human subjects, one of every game’s subject pair was always played by a computer. Every subject played 100 games.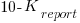 points.
points. ), the Sender gained
), the Sender gained  points (i.e., a -5 point penalty),
points (i.e., a -5 point penalty), , averaged over all 116 subject’s mean) for a given number of red marbles actually seen by the Sender; vertical lines show one standard deviation, calculated over the mean of all subjects (
, averaged over all 116 subject’s mean) for a given number of red marbles actually seen by the Sender; vertical lines show one standard deviation, calculated over the mean of all subjects (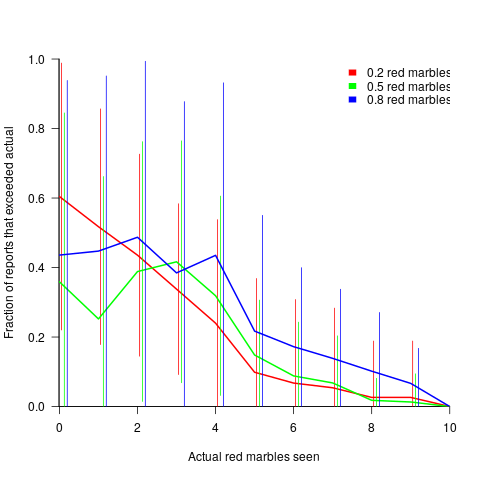

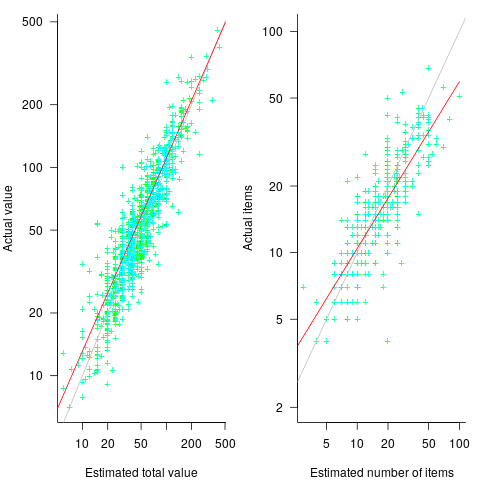
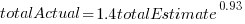 , which differs from
, which differs from 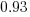 , is at the upper range of those seen for software task estimates.
, is at the upper range of those seen for software task estimates.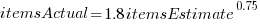 . This pattern, of underestimating small values and overestimating large values is seen in software task estimation, but the exponent of
. This pattern, of underestimating small values and overestimating large values is seen in software task estimation, but the exponent of 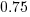 is much smaller.
is much smaller. , in a model for total value produces a slightly better fitting model:
, in a model for total value produces a slightly better fitting model: 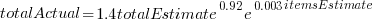 , which explains 83% of the variance in the data (use of a shopping list had a relatively small impact).
, which explains 83% of the variance in the data (use of a shopping list had a relatively small impact).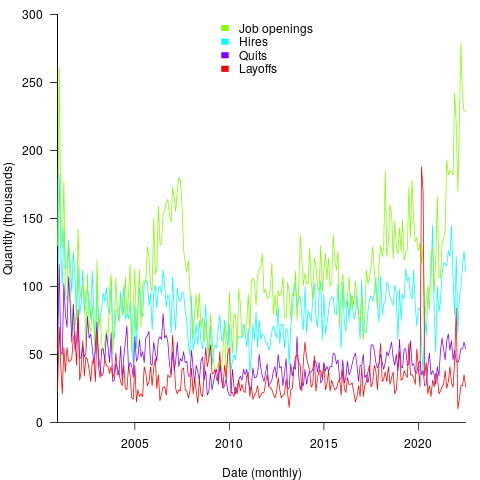


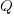 (the derivation assumes that the average quantity in stock is
(the derivation assumes that the average quantity in stock is 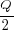 ), it is given by:
), it is given by: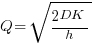 , where
, where 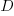 is the quantity consumed per year,
is the quantity consumed per year, 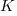 is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods),
is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods), 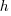 is the annual holding cost per item.
is the annual holding cost per item. items, and it takes
items, and it takes 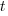 seconds to decide whether a given item should be implemented next, and
seconds to decide whether a given item should be implemented next, and 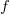 is the fraction of items scanned before one is selected: the average decision time per item is:
is the fraction of items scanned before one is selected: the average decision time per item is: 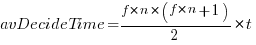 seconds. For example, if
seconds. For example, if 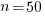 , pulling some numbers out of the air,
, pulling some numbers out of the air, 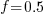 , and
, and 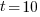 , then
, then 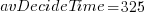 , or 5.4 minutes.
, or 5.4 minutes.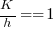 , then
, then 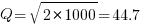 .
.